Excerpted from A Dictionary of Fabulous Beasts, by Richard Barber and Anne Riches and Numbers, by David Wells.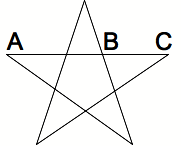

Number: 1.61803 39887 49894 84820 45868 34365 63811 77203 09179 80576…

The Divine Proportion

The Divine Proportion or the Golden Ratio, equal to (sqrt(5)+1)/2.

In the pentagram, which the Pythagoreans regarded as a symbol of health, the ratio of AB to BC is the Golden Ratio.

Euclid in his Elements calls this division ‘in the extreme and mean ratio’ and used it to construct first a regular pentagon, then the two most complex Platonic solids, the dodecahedron, which has 12 pentagonal faces, and the icosahedron, which is its dual.  The mystical significance of these beautiful polyhedra to the Greeks was naturally transferred to the Golden Ratio.

If a rectangle is drawn whose sides are in the Golden Ratio, it may be divided into a square and another, similar, rectangle.  This process may be repeated ad infinitum. It is possible to draw an equiangular spiral through successive vertices of the sequence of rectangles.

The Golden Ratio, Φ, itself is intimately related to the Fibonacci sequence.  Like Φ², the higher powers of Φ can all be expressed very simply in terms of Φ.  Each power is the sum of the 2 previous powers, and the coefficiencts form the Fibonacci sequence over again, as do the integer parts of the powers.

(The Golden Ratio is often found in nature, in the spiral structure of sea shells and in the branches of plants and trees.  See this Wikipedia article for more information.)

Beast: Anaye

The Anaye or Alien Gods of Navaho Indian myth are giants and monsters born of women without intervention of men.  They include Thelgeth, who was headless and hairy, Tsanahale, harpy-like with feathered back, the Binaye Ahani, twins without legs or arms who slew with their eyes, and a nameless monster whose hair grew into the rock so that it could not fall from the cliff where it lived, and which preyed on travellers.  They were all slain by the son of the water and the son of the sun, except for Old Age, Cold, Poverty, and Famine; these were allowed to live on, lest men should cease to honour the gods who protected them against these woes.

Excerpted from A Dictionary of Fabulous Beasts, by Richard Barber and Anne Riches and Numbers, by David Wells.

Number: 0.7404…

pi/sqrt(18)

How closely can identical spheres be packed together?  The obvious way is to arrange one layer on a plane so that each sphere touches 6 others, and then arrange adjacent layers, so that each sphere touches 3 others in each layer (12 in all) and so on.  However, no mathematician has been able to prove this ‘obvious’ fact.

If that were the closest packing, the density would be this number.

‘Many mathematicians believe, and all physicists know, that the density cannot exceed pi/sqrt(18).’ [Rogers]

Beast: Amphisbaena

A two-headed creature, sometimes shown with feathers, but described as a snake by Pliny and by Lucan in his description of the terrors of the African desert in the Pharsalia.  When one head was asleep, the other remained awake, particular while hatching eggs; in this case the head on duty woke up the other one when it was time for it to take over.  Curiously enough, it proves to be a real animal, a limbless lizard which can move both backwards and forwards, and which rears its tail if frightened, pretending that it is a second head.

A little while ago, I found a couple of books in a local used book store that I thought were pretty cool and that I thought I’d post little tidbits from, from time to time.

The first book is A Dictionary of Fabulous Beasts, by Richard Barber and Anne Riches.  The second is Numbers, by David Wells.

Beast: Aigamuchas:

A creature which lived in the Kalahari desert with eyes on the top of its feet and thin pointed teeth as long as a man’s finger.  If these creatures wanted to know what was happening behind them they went on hands and knees with one foot lifted so that they could see backwards.  They hunted men as if they were zebras and ate them.

Number: 5.256946404860…

The approxximate ‘volumes’ of the unit radius ‘spheres’ in dimensions from 1 upwards are:

The volume is a maximum in 5 dimensions, and declines thereafter.  If however the dimension is regarded as a real variable, able to take non-integral values, then the maximum volume occurs in ‘space’ of this dimension, 5.256… The volume is then 5.277768… compared to the volume in 5 dimensions of 5.263789… [David Singmaster]

(More information about n-spheres can be found here.)